আপনিও যদি ষষ্ঠ শ্রেনীর কষে দেখি 1.2 এর সমাধান খুজছেন তাহলে আপনি একেবারে সঠিক জায়গায় এসেছেন, নিচে আপনি Class 6 Kose Dekhi 1.2 সমস্ত সমস্যার সমাধান পেয়ে যাবেন। এই অনুশীলনে তোমাদের গ.সা.গু ও ল.সা.গু উপরে অঙ্ক আছে।
Class 6 Kose Dekhi 1.2 Bengali | কষে দেখি 1.2
1. মনে মনে করি
(a) শূন্য ছাড়া 5 -এর 6 টি গুণিতক খুঁজি।
শূন্য ছাড়া 5 -এর গুনিতক 5, 10, 15, 20, 25 ও 30
(b) 7-এর 3টি গুণিতক খুঁজি যারা 50-এর বড়ো।
7-এর গুণিতক 56, 63 ও 70
(c) দুটি 2 অঙ্কের সংখ্যা ভাবি যারা 4-এর গুণিতক।
4-এর গুণিতক 20 ও 24
(d) 4 কোন কোন সংখ্যার উৎপাদক বা গুণনীয়ক হতে পারে এমন তিনটি সংখ্যা লিখি।
4 সংখ্যাটি 16, 20, 24 সংখ্যাগুলির উৎপাদক হতে পারে।
(f) এমন দুটি সংখ্যা খুঁজি যাদের ল.সা.গু. 12 এবং যাদের যোগফল 10।
4 ও 6 সংখ্যা দুটির ল.সা.গু. 12 এবং যোগফল 10।
2 . (a) 14-এর মৌলিক উৎপাদক কী কী ?
14-এর মৌলিক উৎপাদক 2, 7
(b) সবচেয়ে ছোটো মৌলিক সংখ্যা কী?
উঃ সবচেয়ে ছোটো মৌলিক সংখ্যা হল 2
(c) কোন্ সংখ্যা মৌলিকও নয়, আবার যৌগিকও নয়?
উঃ 1 মৌলিকও নয়, আবার যৌগিকও নয়
3 . (A) 42 কোন্ কোন্ সংখ্যার গুণিতক — (a) 7 (b) 13 (c) 5 (d) 6
উঃ অর্থাৎ 42 এর গুনিতক হল 7 ও 6
(B) 11 কোন সংখ্যার গুণনীয়ক — (a) 101 (b) 111 (c) 121 (d) 112
উঃ 121 এর গুণনীয়ক হল 11
4. সংখ্যাজোড়ার মধ্যে কোনগুলি পরস্পর মৌলিক সংখ্যা দেখি : (a) 5, 7 (b) 10, 21 (c) 10, 15 (d) 16, 15
(a) 5, 7
5 এবং 7—দুটিই মৌলিক, এবং 1 ছাড়া কোনো সাধারণ গুণনীয়ক নেই।
➡️ পরস্পর মৌলিক
(b) 10, 21
10-এর গুণনীয়ক: 1, 2, 5, 10
21-এর গুণনীয়ক: 1, 3, 7, 21
সাধারণ গুণনীয়ক = 1
10 এবং 21— 1 ছাড়া কোনো সাধারণ গুণনীয়ক নেই।
➡️ পরস্পর মৌলিক
(c) 10, 15
10-এর গুণনীয়ক: 1, 2, 5, 10
15-এর গুণনীয়ক: 1, 3, 5, 15
সাধারণ গুণনীয়ক = 1 এবং 5
10 এবং 15— 1 ছাড়া অন্য সাধারণ গুণনীয়ক হল 5।
➡️ পরস্পর মৌলিক নয়
(d) 16, 15
16-এর গুণনীয়ক: 1, 2, 4, 8, 16
15-এর গুণনীয়ক: 1, 3, 5, 15
সাধারণ গুণনীয়ক = 1
16 এবং 15— 1 ছাড়া কোনো সাধারণ গুণনীয়ক নেই।
➡️ পরস্পর মৌলিক
5. এমন দুটি যৌগিক সংখ্যা খুঁজি যারা পরস্পর মৌলিক।
(8,15) ও (9,10) এখানে দুটি যৌগিক সংখ্যা দেওয়া হলো, যারা পরস্পর মৌলিক —অর্থাৎ যাদের গ.সা.গু = 1
8 এর গুণনীয়ক: 1, 2, 4, 8
15 এর গুণনীয়ক: 1, 3, 5, 15
➡️ সাধারণ গুণনীয়ক শুধু 1 → তাই পরস্পর মৌলিক।
9 এর গুণনীয়ক: 1, 3, 9
10 এর গুণনীয়ক: 1, 2, 5, 10
➡️ সাধারণ গুণনীয়ক শুধু 1 → তাই পরস্পর মৌলিক।
6. (a) পরস্পর মৌলিক সংখ্যার গ.সা.গু. কত লিখি।
(b) পরস্পর মৌলিক সংখ্যার ল.সা.গু. কত লিখি।
উঃ (a) পরস্পর মৌলিক সংখ্যার গ.সা.গু. 1
(b) পরস্পর মৌলিক সংখ্যার ল.সা.গু. হল সংখ্যাদুটির গুণফল
Class 6 Kose Dekhi 1.2
7. নীচের সংখ্যাগুলি 1 এবং মৌলিক উৎপাদকে বিশ্লেষণ করে গ.সা.গু. খুঁজি —
(a) 22, 44
22 -এর মৌলিক উৎপাদক =
44 -এর মৌলিক উৎপাদক =
22,44 -এর গ.সা.গু. =
(b) 54, 72
54 -এর মৌলিক উৎপাদক =
72 -এর মৌলিক উৎপাদক =
54, 72 -এর গ.সা.গু. =
(c) 27,64
27 -এর মৌলিক উৎপাদক =
64 -এর মৌলিক উৎপাদক =
27, 64 -এর গ.সা.গু. =
(d) 36, 30
36 -এর মৌলিক উৎপাদক =
30 -এর মৌলিক উৎপাদক =
36, 30 -এর গ.সা.গু. =
(e) 28, 35, 49
28 -এর মৌলিক উৎপাদক =
35 -এর মৌলিক উৎপাদক =
49 -এর মৌলিক উৎপাদক =
28, 35, 49 -এর গ.সা.গু. =
(f) 30, 72, 96
30 -এর মৌলিক উৎপাদক =
72 -এর মৌলিক উৎপাদক =
96 -এর মৌলিক উৎপাদক =
30, 72, 96 -এর গ.সা.গু. =
9. নীচের সংখ্যাগুলি মৌলিক উৎপাদকে বিশ্লেষণ করে ল. সা. গু. খুঁজি |
(a) 25, 80
25 -এর মৌলিক উৎপাদক =
80 -এর মৌলিক উৎপাদক =
25, 80 -এর ল.সা.গু.
(b) 36, 39
36 -এর মৌলিক উৎপাদক =
39 -এর মৌলিক উৎপাদক =
36, 39 -এর ল.সা.গু.
(c) 32, 56
32 -এর মৌলিক উৎপাদক =
56 -এর মৌলিক উৎপাদক =
32, 56 -এর ল.সা.গু.
(d) 36, 48 এবং 72
36 -এর মৌলিক উৎপাদক =
48 -এর মৌলিক উৎপাদক =
72 -এর মৌলিক উৎপাদক =
36, 48 এবং 72 -এর ল.সা.গু.
(e) 25, 35 এবং 45
25 -এর মৌলিক উৎপাদক =
35 -এর মৌলিক উৎপাদক =
45 -এর মৌলিক উৎপাদক =
25, 35 এবং 45 -এর ল.সা.গু.
(f) 32, 40 এবং 84
32 -এর মৌলিক উৎপাদক =
40 -এর মৌলিক উৎপাদক =
84 -এর মৌলিক উৎপাদক =
32, 40 এবং 84 -এর ল.সা.গু.
10. সংখ্যাজোড়ার মধ্যে কোনগুলি পরস্পর মৌলিক খুঁজি—
(a) 47, 23
47 =
23 =
47, 23-এর গ.সা.গু. = 1
1 ছাড়া আর অন্য কোনো সাধারণ উৎপাদক নেই,
47 ও 23 পরস্পর মৌলিক সংখ্যা
(b) 25, 9
25 =
9 =
47, 23-এর গ.সা.গু. = 1
1 ছাড়া আর অন্য কোনো সাধারণ উৎপাদক নেই,
25 ও 9 পরস্পর মৌলিক সংখ্যা
(c) 49, 35
49 =
35 =
47, 23-এর গ.সা.গু. = 7
1 ছাড়া আর অন্য সাধারণ উৎপাদক হল 7 তাই,
49 ও 35 পরস্পর মৌলিক সংখ্যা নয়
(d) 36, 54
36 =
54 =
47, 23-এর গ.সা.গু. = 9
1 ছাড়া আর অন্য সাধারণ উৎপাদক হল 3,2 তাই,
36 ও 54 পরস্পর মৌলিক সংখ্যা নয়
11 . সংক্ষিপ্ত ভাগ পদ্ধতিতে নীচের সংখ্যাগুলির গ.সা.গু. ও ল.সা.গু. নির্ণয় করি —
(a) 33 এবং 132

33 ও 132 -এর গ.সা.গু. =
33 ও 132 -এর ল.সা.গু. =
(b) 90 এবং 144
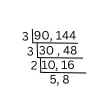
90 ও 144 -এর গ.সা.গু. =
90 ও 144 -এর ল.সা.গু. =
(c) 32, 40 এবং 72
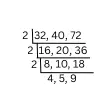
32, 40 ও 72 -এর গ.সা.গু. =
32, 40 ও 72 -এর ল.সা.গু. =
(d) 28, 49 এবং 70

28, 49 ও 70 -এর গ.সা.গু. =
28, 49 ও 70 -এর ল.সা.গু. =
12. সবচেয়ে ছোটো সংখ্যা খুঁজি যা 18, 24 ও 42 দিয়ে বিভাজ্য।
18, 24 ও 42 -এর ল.সা.গু.
∴ সবচেয়ে ছোটো সংখ্যাটি হল 504 যা 18, 24, 42 দিয়ে বিভাজ্য।
13. সবচেয়ে বড়ো সংখ্যা খুঁজি যা দিয়ে 45 ও 60-কে ভাগ করলে কোনো ভাগশেষ থাকবে না।
45 =
60 =
45 ও 60 -এর গ.সা.গু =
∴ 15 দিয়ে 45 ও 60-কে ভাগ করলে কোনো ভাগশেষ থাকবে না।
14. দুটি সংখ্যার ল.সা.গু. ও গ.সা.গু. যথাক্রমে 252 ও 6; সংখ্যা দুটির গুণফল কত হিসেব করি।
দুটি সংখ্যার গুনফল = ল.সা.গু গ.সা.গু
=
∴ সংখ্যা দুটির গুণফল 1512
15. দুটি সংখ্যার গ.সা.গু. ও ল.সা.গু. যথাক্রমে 8 ও 280; একটি সংখ্যা 56 হলে অপর সংখ্যাটি কত হিসাব করি।
দুটি সংখ্যার গুনফল = ল.সা.গু গ.সা.গু
অপর সংখ্যা =
=
একটি সংখ্যা 56 হলে অপর সংখ্যাটি 40
16. দুটি সংখ্যার গ.সা.গু. 1; সংখ্যা দুটি লিখি।
= পরস্পর মৌলিক সংখ্যার গ.সাগু 1
17. 48টি রসগোল্লা ও 64টি সন্দেশ কোনোটি না ভেঙে সবচেয়ে বেশি কতজনকে সমান সংখ্যায় দেওয়া যাবে দেখি।
48 =
64 =
48 ও 64 -এর গ.সা.গু =
48টি রসগোল্লা ও 64টি সন্দেশ কোনোটি না ভেঙে সবচেয়ে বেশি 16 জনকে সমান সংখ্যায় দেওয়া যাবে
18. বিভাস ও তার বন্ধুরা মিলে 8 জন অথবা 10 জন করে সদস্য নিয়ে নাটকের একটি দল তৈরির কথা ভাবল। কমপক্ষে কতজন থাকলে উভয়প্রকার দল তৈরি করতে পারবে হিসেব করি।
8 =
10 =
8 ও 10 -এর ল.সা.গু =
কমপক্ষে 40 জন থাকলে উভয়প্রকার দল তৈরি করতে পারবে ।
19. যদুনাথ বিদ্যামন্দির স্কুলের ষষ্ঠ শ্রেণির ছাত্রছাত্রীদের, স্কুলের বাগানে লাগানোর জন্য পঞ্চায়েত থেকে ফুলের চারা পাঠিয়েছে। হিসেব করে দেখা গেল চারাগুলিকে 20টি, 24টি বা 30টি সারিতে লাগালে প্রতিক্ষেত্রে প্রতিসারিতে সমান চারা থাকে। পঞ্চায়েত থেকে কমপক্ষে কতগুলি চারা পাঠিয়েছিল হিসেব করে দেখি।
20 =
24 =
30 =
20, 24 ও 30 -এর ল.সা.গু
পঞ্চায়েত থেকে কমপক্ষে 120 গুলি চারা পাঠিয়েছিল।
20. একটি ইঞ্জিনের সামনের চাকার পরিধি 14 ডেসিমি. এবং পিছনের চাকার পরিধি 35 ডেসিমি.। কমপক্ষে কত পথ গেলে চাকা দুটি একই সঙ্গে পূর্ণসংখ্যক বার ঘোরা সম্পূর্ণ করবে হিসাব করি।
14 =
35 =
14 ও 35 -এর ল.সা.গু =
কমপক্ষে 70 ডেসিমি. পথ গেলে চাকা দুটি একই সঙ্গে পূর্ণসংখ্যক বার ঘোরা সম্পূর্ণ করবে।

